طريقة جديدة لتسهيل حلّ المعادلات التربيعية

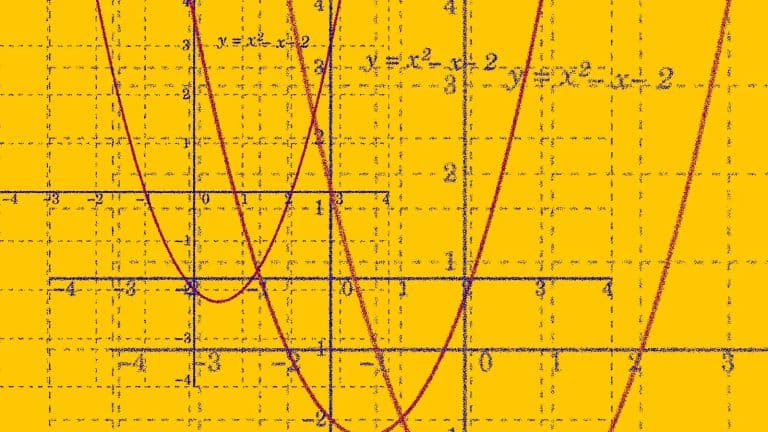
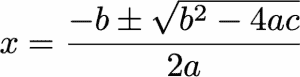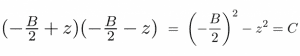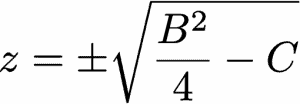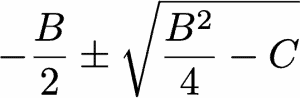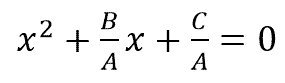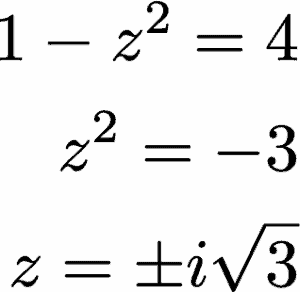كان البابليون القدماء شعباً مذهلاً. ومن بين إنجازاتهم الرائعة الكثيرة، اكتشافُهم لحلٍّ رياضيّ شهير حالياً لمشكلةٍ مزعجة، ألا وهي: دفع الضرائب.

وكانت المشكلة بالتحديد بالنسبة للعامل العادي في بابل تتمثل في السؤال التالي: من أجل سداد قيمة ضريبةٍ معلومة عن طريق المحصول الزراعي، ما الزيادة اللازمة في مساحة حقلي حتى أتمكن من دفعها؟

يمكن كتابة هذه المشكلة في شكل معادلة تربيعية على النحو التالي:

ويتم حلها وفق الصيغة التالية:

اليوم، وبعد مرور 4000 عام، أصبحت هذه الصيغة محفورةً في عقول الملايين من الناس بفضل أسلوب تدريس الرياضيات في جميع أرجاء الكوكب.

غير أنَّ عدداً أقلّ بكثير من الأشخاص يستطيع استنتاج هذا الحل. وهذا أيضاً يعود إلى أسلوب تعليم الرياضيات؛ إذ يعتمد الاستنتاج المُعتاد على طريقةٍ رياضية تسمى "إكمال المربع"، وهي أبعد ما تكون عن البديهية. وفي الواقع، بعد البابليين، استغرق علماء الرياضيات قروناً كثيرة ليكتشفوا هذه الطريقة.

وقبل هذه الطريقة وبعدها، اكتشف الرياضيون مجموعةً واسعة من الطرق الأخرى لاستنتاج صيغة الحل، إلا أن جميع هذه الطرق كانت صعبةً وغير بديهية؛ لذلك من السهل تصوُّر أن علماء الرياضيات قد استنفدوا هذه المشكلة، ولا يمكن أن تكون هناك طريقةٌ أفضل لاستنتاج الصيغة التربيعية.

وهنا يتدخل بوشين لو، وهو عالم رياضيات في جامعة كارنيجي ميلون في بيتسبيرج، الذي وجد مقاربة أبسط يبدو أن الجميع قد غفل عنها لمدة 4000 عام.

لا تعتمد مقاربة لو على إكمال المربع أو أية حيلٍ رياضية معقدة. في الحقيقة، إنها من البساطة بمكان بحيث إنه يمكن أن تَصلُح كمنهجٍ عام بحدِّ ذاتها؛ مما يعني أن الطلاب لن يضطروا لتذكٌّر الصيغة إطلاقاً. يقول لو: "قد تتمكن طريقة الاستنتاج هذه من إزالة الغموض الذي يكتنف الصيغة التربيعية بالنسبة للطلاب في جميع أنحاء العالم".

إنَّ النهج الجديد واضحٌ ومباشر؛ حيث يبدأ بافتراض أن المعادلة التربيعية لها حلان، أو جذران. فإذا أسميناهما R وS فيمكننا كتابتها على الشكل التالي:

لاحِظ أن الجانب الأيمن يساوي 0 عندما x=R أو عندما x=S. وهذا ما نعنيه بالجذور.

ثم من خلال إجراء عملية الضرب في الطرف الأيمن من المعادلة نحصل على:

وهذا يتحقق عندما: (-B=R+S)، و(C=RS).

وهنا تأتي الخطوة الذكية؛ حيث يشير لو إلى أن مجموع الجذرين R وS يكون مساوياً لـ -B إذا كان متوسطهما الحسابي مساوياً لـ -B/2.

يقول لو: "إذن فنحن نبحث عن عددين من الشكل -B/2±z، حيث z هي كمية غير معلومة مفردة". عندها نستطيع أن نضرب هذين العددين معاً للحصول على التعبير الرياضي لـ C. وبالتعويض نحصل على:

ومع بعض الترتيب نحصل على:

 

ما يعني أن حل المعادلة التربيعية هو:

وهكذا نكون قد استنتجنا صيغة حلّ المعادلة التربيعية!

ويمكن استخلاص النسخة الأكثر عمومية من خلال قسمة المعادلة:

على A، فينتج:

ثم نكرر العملية أعلاه.

يمثل هذا الأسلوب تحسيناً كبيراً على الطريقة السابقة، ويبيِّن لو السببَ من خلال مثالٍ بسيط.

مثال: أوجد جذور المعادلة التربيعية التالية:

وفقاً للطريقة التقليدية، يجب إيجاد قيم A، وB، وC، وإدخالها في الصيغة التربيعية. لكنَّ نهج لو يقوم بحلها بشكلٍ بديهي. تتمثل الخطوة الأولى بالتفكير في أنَّ جذري المعادلة يجب أن يكونا مساويين لـ -B/2±z = 1±z

وبما أن جداء الجذرين يجب أن يكون مساوياً لـ C=4، يمكننا إذن أن نكتب:

وبالتالي فالجذران هما:

إنَّ محاولة حل المشكلة نفسها باستخدام الطريقة التقليدية أكثر صعوبةً بكثير. فلتجربها بنفسك! بينما الطريقة الجديدة أسهل بكثير وأكثر بديهية، لا سيما أنها لا تتطلب حفظ الصيغة بتاتاً.

ويكمن التساؤل المثير للاهتمام في السبب وراء عدم تفكير أيّ أحدٍ بهذه الطريقة من قبل. لقد بحث لو في تاريخ الرياضيات عن طريقة تشبه طريقته بلا طائل؛ حيث راجع الأساليب التي طوّرها البابليون القدماء والصينيون والإغريق والهنود والعرب بالإضافة إلى علماء الرياضيات الحديثين منذ عصر النهضة وحتى اليوم. ولا يبدو أن أياً منهم قد جاء بطريقة كهذه، على الرغم من أن الجبر فيها بسيطٌ ومعروف منذ قرون.

لماذا الآن؟ يعتقد لو أن السبب متعلِّق بالطريقة التي تثبت فيها الطريقة التقليدية أن للمعادلة التربيعية جذرين؛ حيث يقول: "ربما يعود السبب إلى أن من المنطقي رياضياً إجراء التضمين العكسي؛ فالمعادلة التربيعية لها دائماً جذران، مجموعهما يساوي −B وجداؤهما يساوي C".

إن لو، وهو مدرس رياضيات وناشطٌ مشهور بعض الشيء في تبسيط الرياضيات للعامة، قد اكتشف أسلوبه أثناء تحليل مناهج الرياضيات لطلاب المدراس بهدف تطوير طرائق شرحٍ جديدة؛ حيث توصَّل إلى طريقة الاستنتاج خلال هذه العملية.

والسؤال المطروح الآن هو: إلى أي مدى ستنتشر طريقته وبأية سرعة؟ ولتسريع اعتمادها، أنتج لو فيديو يشرح فيه أسلوبه. وسواءً اشتهرت طريقته أم لا، فلابدَّ أنها كانت ستثير إعجاب حاسبي الضرائب البابليين.

المرجع: arxiv.org/abs/1910.06709
برهانٌ بسيط للصيغة التربيعية.