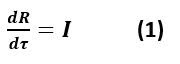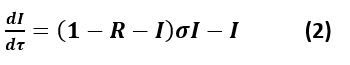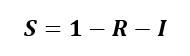من المرجح أن يواصل فيروس كورونا انتشاره بطريقة ديناميكية تختلف بين المناطق تبعاً لمستويات تطبيق إجراءات الابتعاد الاجتماعي والحجر الصحي الذاتي والعزل الجماعي، بالإضافة إلى تأثير المعايير والعادات الاجتماعية السائدة في كل منطقة.
المقالات الأكثر قراءة ضمن تغطية فيروس كورونا المستجد:
- شهادة حية لطبيب مصاب: أعراض الإصابة بفيروس كورونا
- كيف يتمكن فيروس كورونا المستجد من فرض سيطرته على الجسم؟
- هل سيختفي فيروس كورونا مع قدوم فصل الصيف؟
- 15 معلومة خاطئة حول فيروس كورونا
- تحديث: فيروس كورونا قد يبقى على الأسطح حتى 17 يوماً
وفق هذه المعطيات، يمكن استخدام نموذج انتشار الأمراض المعدية المعروف باسم إس آي آر SIR في توقع تطور انتشار الوباء على مستوى محلي خلال فترة محددة من الزمن.
نموذج الأمراض المعدية SIR
يأتي اسم نموذج SIR اختصاراً لـ (المُعرَّضون للإصابة S(t) - المُصابون I(t) - المتعافون R(t))، ويعتمد انتقال العدوى فيه على الاحتكاك بين السكانP فإذا التقى شخص مصاب بشخص مُعرَّض وغير مُحصَّن ضد المرض فإنه ينقل العدوى إليه.

يتم صياغة معادلات تفاضلية في هذا النموذج لتوصيف تزايد نسبة الإصابات والتعافي بين السكان بافتراض أن معدل انتقال العدوى إلى الأشخاص وتعرضهم للفيروس هو موزَّع توزيعاً منتظماً (uniform).
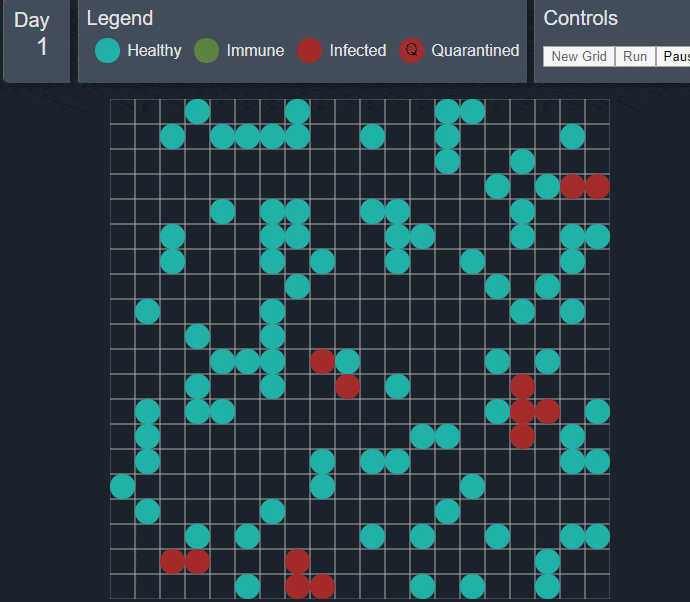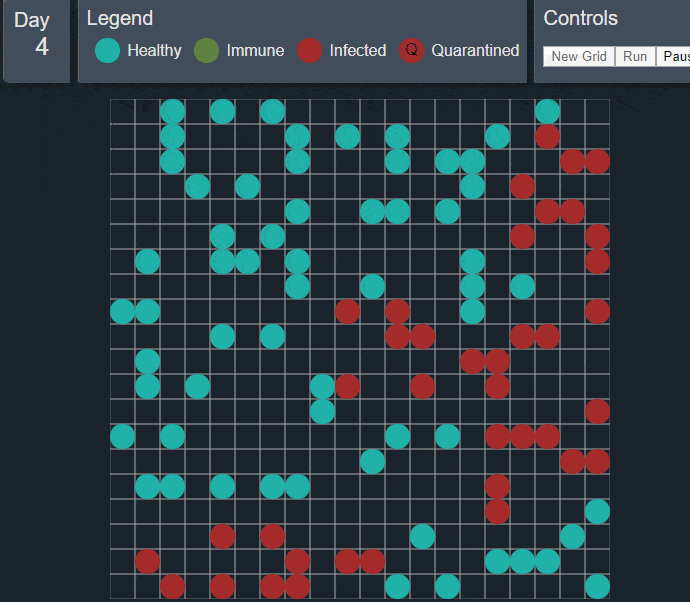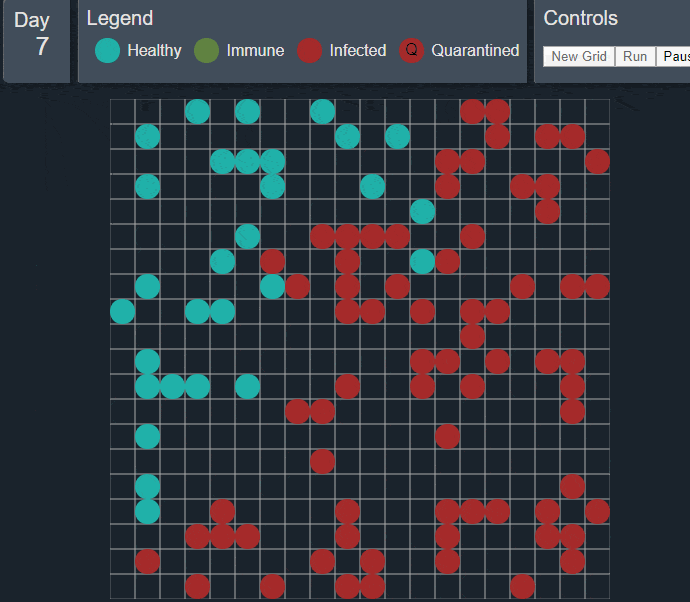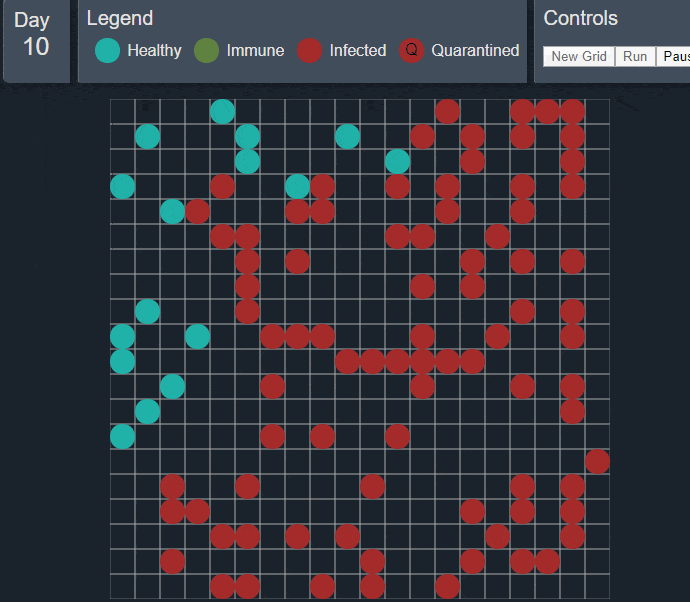
المصدر: https://tachyondecay.github.io/epidemic-simulator/

المصدر: https://tachyondecay.github.io/epidemic-simulator/
وقد قام الباحث الإسباني خافيير غارسيا دو أباجو بإجراء دراسة جديدة نُشرت على موقع Medrxiv، ولم تتم مراجعتها من قِبل الأقران، استند فيها إلى هذا النموذج وقام بإسقاطه على حالة تفشي فيروس كورونا في محاولة لفهم سرعة انتشار الوباء وتأثير الابتعاد الاجتماعي في احتوائه.
التفاصيل الرياضية لنموذج SIR
نرمز بـ T للفترة الزمنية التي يكون خلالها الشخص المصاب ناقلاً للعدوى (ويقدر الباحث في نموذجه أن هذه المدة تتراوح بين أسبوعين إلى أربعة أسابيع في حالة فيروس كورونا)، وt يرمز للزمن بالأيام، عندها يمكن تقديم المتغير τ=t/T، فتكون المعادلة التفاضلية التي تعبر عن تغير نسبة الأشخاص المتعافين هي:
والمعادلة التفاضلية التي تعبر عن تغير نسبة المصابين هي:
حيث:
- R تمثل نسبة الأشخاص المتعافين.
- I تمثل نسبة الأشخاص المصابين.
- σ تمثل عدد الاحتكاكات (contact number) بين الأشخاص.
وبالتالي تكون نسبة الأشخاص المعرضين للإصابة S(t) هي:
أما الشروط الابتدائية لنظام المعادلات التفاضلية من الدرجة الأولى الممثل بالمعادلتين (1) و(2) فهي:
نسبة المتعافين في اليوم صفر عند بداية تفشي الوباء هي R(0)=0.
نسبة المصابين في اليوم صفر ضئيلة جداً أي I(0)<<1.
إسقاط نموذج SIR على تفشي فيروس كورونا
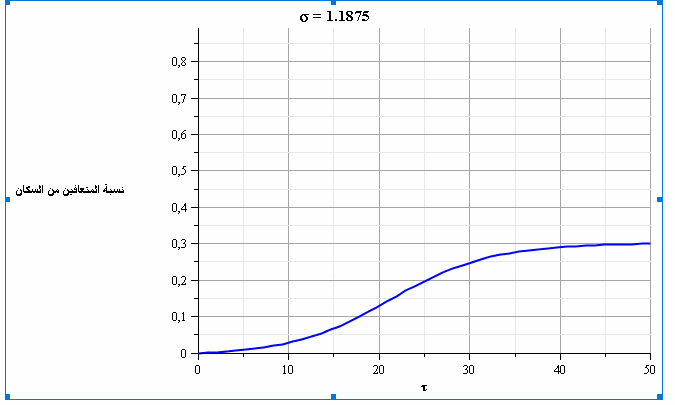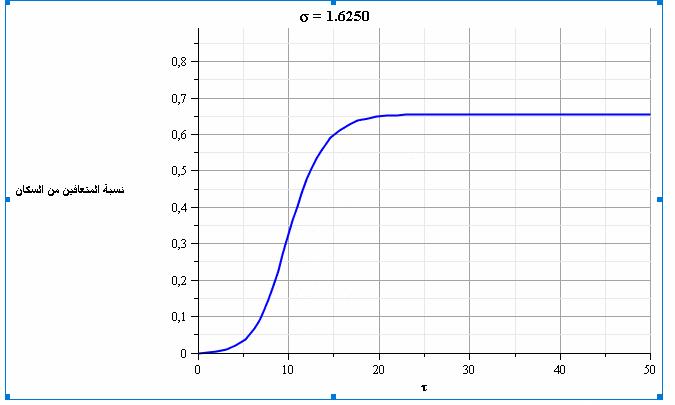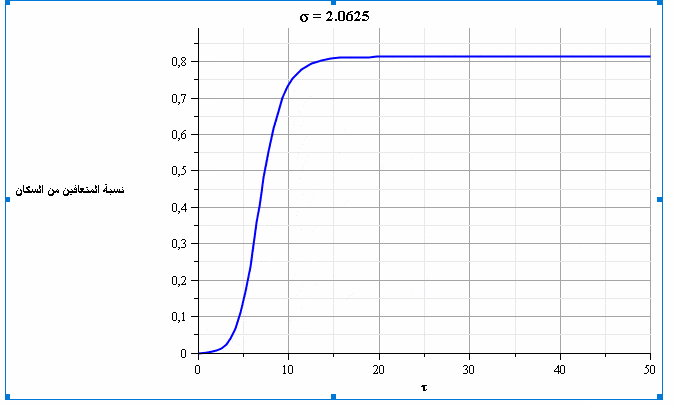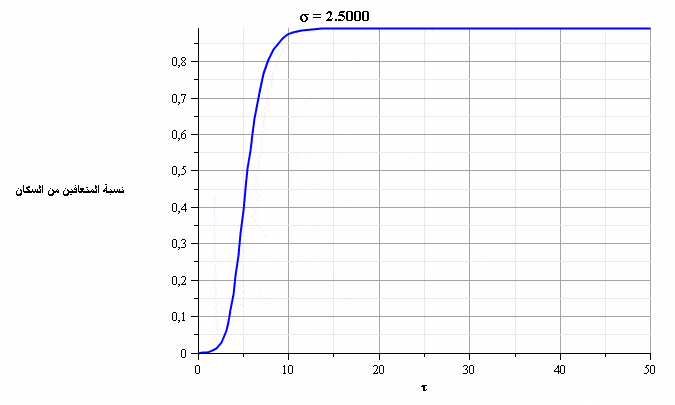
بما أننا نشهد بداية تفشي الفيروس في معظم المناطق، فإن تسارع نسبة الإصابات يعتمد بشكل أساسي على عدد الاحتكاكات بين الأشخاص (σ).
ويقدر الباحث أن قيمة σ تتراوح بين 1.5 (مع فرض إجراءات الابتعاد الاجتماعي) وحتى 3 (من دون اتباع أي سياسات مواجهة)، لكنه يشير إلى عدم توافر بيانات حاسمة حول القيمة الفعلية لهذا العدد، فقد يتأثر بحدوث تحورات في الفيروس مما يستدعي بحثاً أعمق حول هذا الموضوع.
ومن خلال حل المعادلتين السابقتين، نحصل على الشكلين التاليين الذين يمثلان تطور نسبة المصابين والمتعافين بمرور الزمن ومع قيم متغيرة لعدد الاحتكاكات (σ). نلاحظ في الشكل 4 أنه عندما تكون قيمة عدد الاحتكاكات =2.5σ فإن ذروة نسبة الإصابات تتجاوز 20% من السكان.
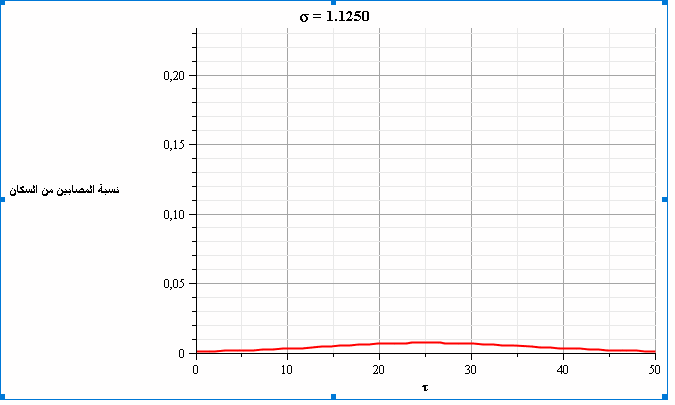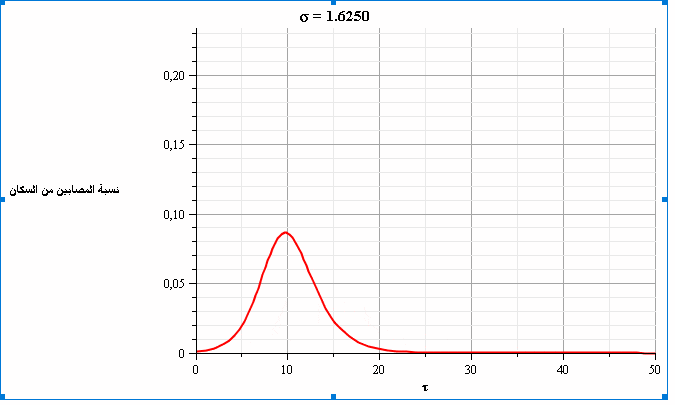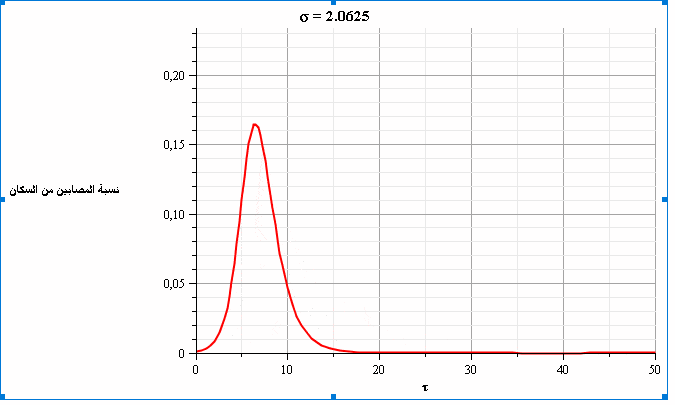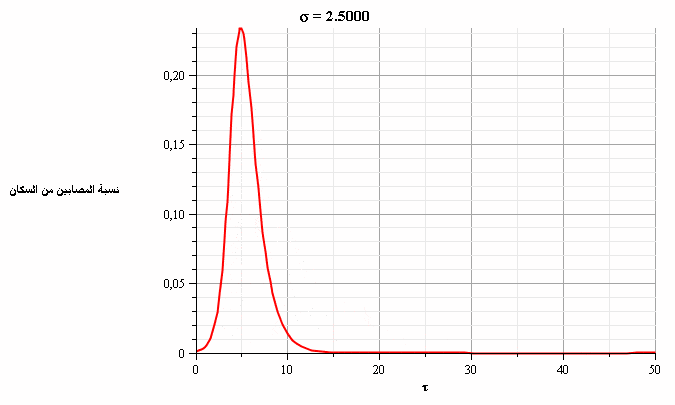
كيف يساعدنا نموذج SIR على فهم انتشار فيروس كورونا؟
يتضح من الشكلين البيانيين أن تطبيق إجراءات الابتعاد الاجتماعي -وبالتالي تقليل قيمة عدد الاحتكاكات- سيؤدي إلى تخفيض ذروة نسبة الإصابات (تسطيح المنحنى) وبالتالي سيقلل من خطورة العدوى بشكل عام؛ حيث سيؤدي ذلك إلى زيادة القدرة على تأمين الرعاية الصحية اللازمة إلى نسبة أكبر من السكان المصابين بالإضافة إلى إمكانية الوصول إلى المناعة الجماعية (مناعة القطيع) عند نسبة أقل من الأشخاص المتعافين.
وفي ضوء هذا النموذج، يمكن النظر إلى الابتعاد الاجتماعي على أنه تخفيض لقيمة عدد الاحتكاكات. لكن يشير الباحث إلى أنه حتى مع تخفيض هذا العدد من 2.5 إلى 1.3، فإن نسبة الإصابات تظل أعلى من طاقة المستشفيات الاستيعابية، مما سيؤدي إلى نسبة وفيات إجمالية تقارب 1.2% من السكان.
والسؤال الذي يطرح نفسه في هذا السياق هو: هل ستتمكن الإجراءات المتخذة في معظم الدول أن تخفض عدد الاحتكاكات إلى ما يقارب أو أقل من 1، بحيث يتم السيطرة على التزايد في عدد الإصابات وإبقاء ذروتها ضمن إمكانيات أنظمتها الصحية إلى أن يتم إنتاج لقاح وتطبيقه للوصول إلى مناعة جماعية؟
وفي الختام، يشير الباحث إلى أن إجراءات العزل والابتعاد الاجتماعي قد تحقق التأثير المطلوب إذا ما تمكنت من الاقتراب بعدد الاحتكاكات إلى قيمة 1. ويقول إنه ينبغي القيام بمزيد من العمل والإضافات إلى هذا النموذج قبل أن نتمكن من تعميمه على مستوى عالمي.
المرجع: https://www.medrxiv.org/content/10.1101/2020.03.17.20037663v1
رياضيات بسيطة حول توسع انتشار كوفيد-19