تستطيع عناصر نظام معقد أن تتزامن بشكل طبيعي مع بعضها البعض، تماماً كما يحدث لفرقة موسيقية يعزف أفرادها من دون مايسترو يقودها، وتُعرف هذه الظاهرة الجماعية باسم التزامن؛ حيث تحدث وفق عدة أشكال في الطبيعة، بدءاً من العصبونات التي تطلق إشاراتها داخل الدماغ في آن واحد، وصولاً إلى اليراعات التي تومض بشكل متزامن موحد في الظلام.
وقد عرف الرياضي كريستيان هيوجينز التزامنَ لأول مرة في 1665، وذلك عندما راقب نوّاسَيْ ساعة معلقَين من نفس المحور الخشبي وهما يتأرجحان بشكل متزامن. ولكن هذه الظاهرة الجماعية لم يتم توصيفها رياضياً حتى 1975، عندما اقترح الفيزيائي الياباني يوشيكي كوراموتو نموذجاً مبسطاً لها، حيث يعبر نموذج كوراموتو عن التزامن في الشبكات الكبيرة، التي تلعب فيها العُقَد دور هزازات تسلك سلوك الساعات، وترتبط مع الهزازات الأخرى في العُقد المجاورة. وبغياب الوصلات بين هذه العقد، يعمل كل هزاز وفقاً لنظامه الخاص من دون أن يتأثر بجيرانه. ولكن عندما ينتقل التفاعل بين العقد المتجاورة إلى قيمة أعلى من عتبة معينة، تبدأ الهزازات بالعمل وفق نفس التردد.
وبالرغم من أن نموذج كوراموتو يصف تزامن الديناميات الخاصة بالعقد المكوِّنة لشبكة معينة على شكل أغراض من المُعقّدات الفائقة عالية المرتبة (Simplicial Complexes) في الشبكة، مثل الوصلات أو المثلثات، إلا أن بإمكانه أيضاً أن يُظهر الإشارات الديناميكية أو "الطوبولوجية" مثل التدفقات.
وهنا يأتي دور بحث جديد أُجريَ بقيادة جامعة كوين ماري في لندن، يحمل عنوان "ديناميات كوراموتو الانفجارية عالية المرتبة للمعقّدات الفائقة"؛ حيث يقدم نوعاً جديداً من نموذج كوراموتو، وهو نموذج عالي المرتبة يجمع ما بين الطوبولوجيا والأنظمة الديناميكية، ويعبر عن خصائص التزامن في الشبكات عالية المرتبة للمرة الأولى. ويُستخدم نموذج كوراموتو لدراسة التزامن في الأنظمة المعقدة التي يتم استخدام الشبكات لتمثيلها رياضياً في أغلب الأحيان، حيث تلعب عناصر النظام دور العُقد، وتمثل الوصلات بين هذه العقد العلاقات القائمة بين عناصر النظام.
بعض من الرياضيات
وقبل مواصلة الحديث عن تفاصيل هذا البحث، دعونا نتطرق أولاً إلى توضيح ما الذي يعنيه المصطلح الرياضي: المُعقّد ذو الرؤوس الفائقة (Simplicial Complex)، أو اختصاراً: المعقد الفائق. وهو مجموعة مكونة من نقاط وقطع مستقيمة، ومثلثات، وهكذا هلم جراً، حيث تشمل مكونات البناء كلَّ نظائر هذه الأشكال الهندسية في فضاء متعدد الأبعاد بُعده n، ويمكن تصور هذه المكونات البنائية على أنها رباعيات وجوه فائقة (hypertetrahedrons). ويمكن تعريفه كما يلي:
إذا كان لدينا مُعقد فائق اسمه K، فهو مجموعة من رباعيات الوجوه الفائقة التي تحقق الشروط التالية:
- كل وجه (سطح) لرباعي وجوه فائق من K ينتمي إلى K أيضاً.
- تقاطع أي اثنين من رباعيات الوجوه الفائقة (s1، s2) ينتميان إلى K، هو وجه (سطح) ينتمي إلى كل من s1 وs2.
ومن الأمثلة على كيفية تمثيل رباعيات الوجوه الفائقة (Simplex) عند ترميزها في فضاء بُعده n، يمكننا توضيح ما يلي:
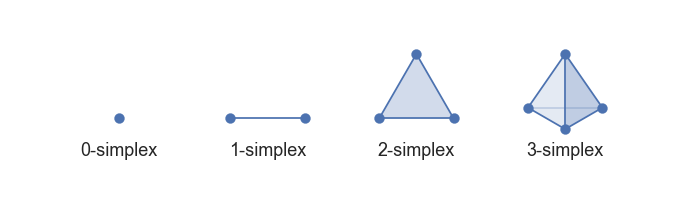
- عندما نقول 0-simplex: فهو يعني نقطة أو عقدة (n=0).
- 1-simplex: تعني قطعة مستقيمة أو وصلة (n=1).
- 2-simplex: تعني مثلثاً.
- 3-simplex: تعني رباعي وجوه.
- 4-simplex: تعني خماسي الخلايا الفائق، وهو غرض رباعي الأبعاد تحدّه خمسٌ من الخلايا رباعية الوجوه، أي أن كل رأس فيه عبارة عن رباعي وجوه.



خماسي خلايا فائق (4-simplex).
يمكن القول إن المعقد الفائق هو تعميم للمبيان (أو البيان graph) في فضاء متعدد الأبعاد، ولهذا تسمى المعقدات من هذا النوع أحياناً "مبيانات زائدية" (المخطط أو المبيان الزائدي: هو تعميم لمفهوم المبيان graph حيث كل ضلع أو وصلة فيه تضم عدة عقد). وتتمثل كتل البناء في المعقد الفائق بالعقد، والوصلات، والمثلثات، ورباعيات الوجوه الفائقة في فضاء متعدد الأبعاد مثل رباعي الوجوه في الفضاء R3.
لماذا هذه المُعقّدات المعقدة؟
في الواقع، ركزت أغلب دراسات التزامن على الشبكات (التمثيل الشبكي)؛ حيث تمثل العقد هزازات ديناميكية تسلك سلوك الساعات، وترتبط مع العقد المجاورة عن طريق وصلات الشبكة. غير أن أغلبية الأنظمة المعقدة تتمتع ببنية أكثر غنى من الشبكات، وتتضمن تفاعلات من مراتب أعلى تحدث بين أكثر من عقدتين. تسمى هذه الشبكات عالية المرتبة بالمُعقّدات الفائقة، وقد أجريت عليها دراسات مكثفة من قِبل الرياضيين الذين يعملون في مجال الطوبولوجيا المتقطعة.
نموذج جديد
وبالعودة إلى الحديث عن البحث الجديد الذي جرى بقيادة البروفيسورة جينيسترا بيانكوني، وهي مختصة بالرياضيات التطبيقية في جامعة كوين ماري في لندن، فهو يقترح شكلاً جديداً عالي المرتبة من نموذج كوراموتو، بحيث يجمع ما بين الطوبولوجيا والأنظمة الديناميكية، وذلك لنمذجة خصائص التزامن في الشبكات عالية المرتبة للمرة الأولى. وقد وجدت الدراسة أن التزامن عالي المرتبة يحدث فجأة، وبطريقة يمكن وصفها بأنها انفجارية، تختلف عن التزامن التدريجي الذي يحدث في نموذج كوراموتو المعياري.
اقترح الباحثون في الدراسة الجديدة شكلاً عالي المرتبة من نموذج كوراموتو يستطيع أن يوصّف التزامن بين هذه الإشارات الطوبولوجية. وبما أن هذه الإشارات الطوبولوجية -مثل التدفقات (أو الجريان)- يمكن أن توجد في الدماغ وشبكات النقل البيولوجية، فقد أشار الباحثون إلى أن هذا النموذج الجديد يمكن أن يكشف عن تزامنات من مراتب أعلى لم تتم ملاحظتها من قبل.
وفيما يتعلق بالأسلوب الذي اتبعه الباحثون للتوصل إلى النموذج الجديد، فقد جمعوا ما بين نظرية هودج (وهي فرع هام من الطوبولوجيا) ونظرية الأنظمة الديناميكية؛ وذلك لإلقاء الضوء على التزامن عالي المرتبة. وباستخدام هذا الإطار النظري، يمكن التعامل مع تزامن الإشارات الديناميكية الطوبولوجية المرافقة للوصلات، مثل التدفقات، أو المرافقة للمثلثات أو لغيرها من كتل البناء الأعلى مرتبة التي تكوّن الشبكات عالية المرتبة. في الواقع، يمكن أن تتزامن هذه الإشارات، ولكن قد تتعذر ملاحظة هذا التزامن من دون تطبيق التحويلات الطوبولوجية الصحيحة.
في الختام
يمكن تشبيه عمل الفريق بتحويل فورييه للإشارات الطوبولوجية لكشف هذا الانتقال نحو التزامن في الأنظمة الحقيقة، مثل الدماغ. ويشير الانتقال المتقطع الذي وجدته الدراسة أيضاً إلى أن ظاهرة التزامن ليست ذاتية الحدوث وحسب، بل تظهر بشكل فجائي أيضاً، ما يكشف أثر الطوبولوجيا في إحداث تغيرات سريعة في القوى المحركة للمنظومات المعقدة، التي تحدث عند بدء الانتقال إلى وضعية التزامن.
وقد تم نشر البحث الجديد في مجلة Physical Review Letters العلمية الخاضعة لمراجعة الأقران، تحت عنوان: ديناميات كوراموتو الانفجارية عالية المرتبة ضمن المعقدات الفائقة.