كان ديفيد دوفينود مشاركاً في مشروع يتضمن بيانات طبية عندما واجه مشاكل بسبب نقيصة كبيرة في الذكاء الاصطناعي.
يعمل دوفينود باحثاً في مجال الذكاء الاصطناعي في جامعة تورونتو، وكان يحاول بناء نموذج للتعلم العميق يقوم بتوقع الحالة الصحية للمريض مع مرور الوقت، غير أن بيانات السجلات الطبية عشوائية بعض الشيء، فقد تزور الطبيب خلال حياتك في أوقات مختلفة لأسباب مختلفة، مما يؤدي إلى انتثار البيانات على فواصل زمنية اعتباطية، وهو ما يسبب مشكلة كبيرة للشبكات العصبونية التقليدية، التي يحتاج تصميمها إلى التعلم من بيانات موزعة على مراحل واضحة من المراقبة، ولهذا فهي ليست صالحة كثيراً لنمذجة العمليات المستمرة، خصوصاً تلك التي يتم قياسها بشكل عشوائي عبر الزمن.
ونتيجة لهذه المشكلة، قام دوفينود وزملاؤه في الجامعة ومعهد فيكتور بتغيير التصميم المعروف للشبكات العصبونية. وقد حاز بحثهم مؤخراً -مع أربعة أبحاث أخرى- على لقب "أفضل بحث" في مؤتمر أنظمة معالجة المعلومات العصبونية، وهو من أكبر اللقاءات حول الذكاء الاصطناعي في العالم.
وتعتبر الشبكات العصبونية بمثابة الآلات الرئيسية التي تُكسب التعلم العميق قدراته الفريدة، وتتألف الشبكة التقليدية من عدة طبقات متتالية مؤلفة من عقد حوسبة بسيطة تعمل بشكل مشترك لكشف الأنماط في البيانات. وقد أدى هذا الانفصال بين الطبقات إلى عجز هذه الشبكات عن نمذجة العمليات المستمرة بفعالية (سنتحدث عن هذا لاحقاً).
ولهذا قام الفريق البحثي بإلغاء فكرة الطبقات بالكامل، وقد أكد دوفينود على أنهم لم يبتكروا الفكرة، بل كانوا فقط السبَّاقين في تطبيقها بشكل معمم. ولفهم كيفية تحقيق هذا المبدأ، لنطَّلع على عمل الطبقات أولاً.
مصدر الصورة: جيف كلون/ صورة شاشة
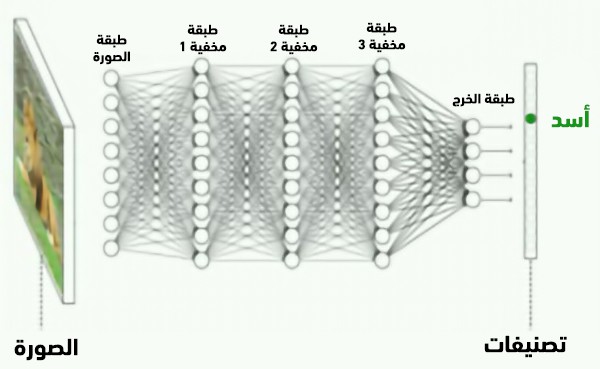
تتضمن عملية تدريب الشبكات العصبونية الأكثر شيوعاً (المعروفة باسم التعليم الموجَّه) تلقيم الشبكة بكميات كبيرة من البيانات المصنفة. ولنفرض أنك ترغب في بناء نظام يقوم بالتعرف على حيوانات مختلفة، بالتالي ستقوم بتلقيم الشبكة العصبونية بصور حيوانات مرفقة بأسمائها، وحينها سيبدأ حل أحجية رياضية جنونية داخل الشبكة؛ حيث تفحص الشبكة جميع الأزواج (صورة-اسم)، وتقوم باستنتاج معادلة تقوم بتحويل الصورة إلى الاسم أو التصنيف بشكل موثوق، وبمجرد أن تحل الأحجية سيمكن استخدام المعادلة مراراً وتكراراً لتصنيف أية صور جديدة للحيوانات، بدقة عالية (ولكن ليست مثالية).
غير أن وضع معادلة واحدة لوصف عملية التحويل هذه بالكامل سيكون عاماً للغاية، وسيؤدي إلى نموذج ذي أداء سيئ، وسيكون أشبه بمحاولة استخدام قاعدة واحدة للتمييز ما بين القطط والكلاب، حيث يمكن القول بأن الكلاب تمتلك آذاناً رخوة، ولكن بعض الكلاب تمتلك آذاناً منتصبة، كما أن بعض القطط تمتلك آذانا رخوة، وسينتهي بك المطاف بشبكة تخلط ما بين الكلاب والقطط بشكل فاقع.
وهنا يأتي دور طبقات الشبكة العصبونية، التي تقوم بتقسيم عملية التحويل إلى عدة خطوات، وتسمح للشبكة بإيجاد سلسلة من المعادلات التي تصف كل منها مرحلة من العملية. فتقوم الطبقة الأولى مثلاً بفحص كل البيكسلات وتستخدم معادلة لانتقاء البيكسلات الأكثر ارتباطاً بالكلاب والقطط، ويمكن أن تقوم طبقة أخرى ببناء أنماط أكبر من مجموعات البيكسلات حتى تكتشف مثلاً الشوارب أو الآذان، ويزداد تعقيد الميزات الموصوفة مع تتابع الطبقات، إلى أن تقوم الطبقة الأخيرة باتخاذ القرار بناء على الحسابات المتراكمة. هذا التتابع يسمح للشبكة العصبونية ببناء نماذج أكثر تعقيداً، ومن ثم يتم تحويلها إلى توقعات أكثر دقة.
وقد لعبت طريقة الطبقات دوراً هاماً في حقل الذكاء الاصطناعي، ولكنها ليست خالية من العيوب؛ فإذا رغبت في نمذجة شيء يتغير بشكل مستمر مع الزمن، يجب أيضاً أن تقوم بتقسيمه إلى خطوات منفصلة. ومن الناحية العملية، وبالعودة إلى مثال النموذج الصحي، سيعني هذا تجميع السجلات الطبية ضمن فترات محددة، مثل أشهر أو سنوات، وهنا تظهر مشكلة عدم الدقة، فإذا زرتَ الطبيب في 11 يناير و16 نوفمبر، فسيتم تجميع البيانات من كلتا الزيارتين ضمن نفس السنة.
يبدو إذن أن أفضل طريقة لنمذجة الواقع هي إضافة المزيد من الطبقات لزيادة الدقة، وقد نفكر مثلاً في تقسيم السجلات إلى أيام أو حتى ساعات، في حال قمت بزيارة الطبيب مرتين في يوم واحد، وإذا أردنا زيادة الدقة إلى أقصى حد ممكن، فقد يعني هذا أن أفضل الشبكات العصبونية لتأدية هذا العمل يجب أن تحتوي على عدد لانهائي من الطبقات لنمذجة تغيرات خطوية بالغة الصغر، وهنا لا بد من أنك بدأت تتساءل فيما إذا كانت هذه الطريقة قابلة حتى للتطبيق.
إذا بدأت تشعر أن هذه المشكلة تبدو مألوفة، فهذا لأنها تطابق تماماً المشاكل التي تم اختراع علم التفاضل والتكامل لحلها؛ حيث يقدم لنا هذا العلم مجموعة جميلة من المعادلات لحساب التغييرات على خطوات بالغة الصغر، أي أنه يوفر علينا كابوس نمذجة التغيرات المستمرة بشكل متقطع، وهو السحر الكامن في بحث دوفينود وزملائه؛ حيث إنه يستخدم معادلات التفاضل والتكامل بدلاً من الطبقات.
وفي الحقيقة، فإن البنية الناتجة لا يمكن حتى أن نسميها بالشبكة، فقد اختفت العقد والوصلات، ولم يعد هناك سوى كتلة واحدة من العمليات الحسابية، ولكن قرر الباحثون -حفاظاً على التقاليد- تسمية هذا التصميم "شبكة أو دي إي ODE"، أي شبكة المعادلات التفاضلية العادية (قد يكون من الأفضل محاولة إيجاد اسم أكثر جاذبية).
إذا بدأت تشعر بالصداع فهذا أمر متوقع، ولهذا يقدم دوفينود مثالاً جميلاً يعبر عن الموضوع بأكمله. لنأخذ مثالاً عن آلة موسيقية ذات أصوات مستمرة (مثل الكمان)، حيث يمكنك أن تزلق إصبعك على طول الوتر لإصدار أي تواتر ترغب فيه، ولنأخذ آلة أخرى ذات أصوات متقطعة ومتمايزة، مثل البيانو، حيث يوجد عدد محدد من المفاتيح تُصدر عددا محدداً من التواترات. تشبه الشبكة العصبونية التقليدية البيانو، حيث لن تستطيع عزف انزلاق موسيقي (أي الانتقال بشكل تدريجي بين النغمات) مهما حاولت، بل يمكنك أن تقرِّبه فقط بعزف سلم متقطع. وحتى لو عدلت البيانو بحيث تصبح التواترات قريبة للغاية من بعضها، سيبقى عزفك سلماً يشبه الانزلاق بشكل تقريبي؛ إذن فإن الانتقال إلى شبكة أو دي إي يشبه الانتقال من البيانو إلى الكمان. قد لا تكون هذه الشبكة هي الأداة المناسبة على الدوام، ولكنها الخيار الأفضل بالتأكيد لإنجاز مهام محددة.
وإضافة إلى نمذجة التغيرات المستمرة، يمكن لهذه الشبكة الجديدة أيضاً أن تغير من مفاهيم محددة في التدريب؛ فبوجود شبكة عصبونية تقليدية، يجب أن تحدد عدد الطبقات التي ترغب في وجودها داخل شبكتك في بداية التدريب، ومن ثم تنتظر حتى انتهاء التدريب لتفقُّد دقة النموذج. أما الطريقة الجديدة فتسمح لك بتحديد الدقة المطلوبة أولاً، ومن ثم ستجد أفضل طريقة لتدريب نفسها ضمن هذا الهامش من الخطأ. ولكن من ناحية أخرى، يمكن معرفة الوقت المطلوب لتدريب شبكة عصبونية تقليدية منذ البداية، في حين أن هذا مستحيل عند استخدام شبكة أو دي إي. يقول دوفينود إن هذه هي التوازنات التي سيضطر الباحثون للتعامل معها عندما يقررون أية تقنية سيستخدمون في المستقبل.
وحالياً، يحوي البحث برهاناً على صحة التصميم، "ولكنه ليس جاهزاً بعد للاستخدام على نطاق واسع" كما يقول دوفينود. وعلى غرار أية تكنولوجيا جديدة يتم اقتراحها في هذا المجال، فإن التصميم ما زال في حاجة إلى مزيد من الدراسة والتجارب والتحسينات حتى يصبح جاهزاً للعمل، غير أن من الممكن أن تُحدث هزة كبيرة في هذا المجال، كما حدث عندما نشر إيان جودفيلو بحثه حول الشبكات التوليدية التنافسية.
يقول ريتشارد زيميل (مدير الأبحاث في معهد فيكتور، ولم يشارك في البحث): "نشأت الكثير من التطورات الهامة في مجال التعلم الآلي من الشبكات العصبونية، ومن المرجح أن هذا البحث سيُطلق موجة من الأعمال المرتكزة عليه، خصوصاً في نماذج السلاسل الزمنية، التي تعتبر أساسية في بعض تطبيقات الذكاء الاصطناعي مثل الرعاية الصحية".
كلمة أخيرة: عندما تصبح شبكات المعادلات التفاضلية العادية ذائعة الصِّيت، لا تنس أنك قرأت عنها لأول مرة هنا.

