هل تستطيع الحواسيب التحقق من صحة حل أي مسألة في زمن معقول؟

يحب العلماء تصنيف كل ما تقع أيديهم عليه، على الأقل في المستوى المجرد. وعلى سبيل المثال، يوجد تصنيف يعتمده الكيميائيون لجميع العناصر في الجدول الدوري، كما يصنف البيولوجيون جميع الكائنات الحية على الأرض ضمن فصائل وأنواع، وفي العقد المنصرم، تمكن الرياضيون بعد بحث طويل من اكتشاف وتصنيف جميع المجموعات البسيطة المنتهية.

أما علماء الحواسيب، فهم يبحثون أيضاً عن النظام والترتيب، ولكن بشكل مختلف بعض الشيء؛ حيث يصنفون المسائل وفقاً لتعقيدها الحسابي. وهنا يجدر بنا التطرق إلى عدد من المفاهيم الأساسية قبل مواصلة الحديث.

نظرية التعقيد

هي النظرية التي تهتم بتحديد الموارد اللازمة لحل مسألة معينة، وفي عالم الحواسيب والخوارزميات، فإن نظرية التعقيد ونظرية الخوارزميات الفعالة تشكلان وجهين لعملة واحدة؛ حيث يمكن اعتبار مسألة خوارزمية معينة أنها محلولة، إذا كان هناك خوارزمية معروفة بأنها لا تستهلك قدراً أكبر بكثير من الموارد التي ثبت أنها تلزم لحل المسألة.

الخوارزمية الحدودية

وهي الخوارزمية التي يكون زمن تشغيلها حاسوبياً في أسوأ حالاته محدوداً بكثير حدود من مرتبة طول الدخل (عدد المعاملات الوسيطة).

صف التعقيد (P)

وهو صف التعقيد الذي يحتوي على جميع المسائل التي يمكن حلها باستخدام خوارزميات (آلة تورنغ) حدودية.

صف التعقيد (NP)

وهو صف التعقيد الذي يحتوي على جميع مسائل القرار أو معالجة اللغات التي يمكن حلها باستخدام آلة تورنغ غير حتمية (nondeterministic) خلال زمن حدودي.

حل المسائل حاسوبياً

وجد علماء الحواسيب من قبل أن بعض المهام يمكن حلها بسهولة فائقة باستخدام الحواسيب؛ حيث إن الزمن الذي تستغرقه الحواسيب لحل المسألة يتزايد ببطء (وهو ما يعرف بتزايد كثير الحدود، أو التزايد الحدودي) مع تزايد حجم المسألة. ومن وجهة نظر علماء الحواسيب، فإن مهام الحوسبة من هذا النوع تنتمي إلى صف التعقيد (P).

أما المسائل التي يمكن التحقق من صحتها، حتى لو كانت صعبة الحل، فهي تنتمي إلى صف التعقيد NP (وما زال من غير الواضح ما إذا كان NP أكبر حقاً من P). وأحد أبرز الأمثلة على هذه المرتبة هي أحجية سودوكو المعقدة؛ حيث من الصعب العثور على الحل الصحيح، في حين أن التحقق من صحة الحل المطروح أمر سهل للغاية.

غير أن هذين الصفين (P, NP) لا يمثلان سوى البداية وحسب؛ فقد قام علماء الحواسيب ببناء تراتبيّة لصفوف التعقيد، بدءاً من أبسطها وانتهاء بأشدها تطلباً للموارد. وقد جلبت الحواسيب الكمومية معها بعض التغييرات، فقد سمحت باستخدام إستراتيجيات جديدة للتحقق من صحة حل مسألة ما.

مسألة كليك

هذه المسألة -التي تُعرف أيضاً بمشكلة المخطط الكامل ضمن بيان- تصف مهمة العثور على العدد الأقصى من العقد المتجاورة بشكل مباشر ضمن بيان ما (graph)، وتنتمي إلى صف التعقيد NP، وتبين الصورة خوارزمية لحل هذه المسألة، وفي هذه الحالة، فإن عدد كليك يساوي 4.

لطالما كان أحد أهم الأسئلة المفتوحة في أبحاث التعقيد هو مدى تعقيد المسألة التي يستطيع الحاسوب التحقق من حلها في زمن معقول، مثل الزمن من النمط الحدودي (من مرتبة كثير حدود). وقد اكتشف فريق بقيادة زينجفينج جي من جامعة التكنولوجيا في سيدني إجابة مفاجئة أطلقت موجة من الحماسة في أوساط الخبراء. ووفقاً لهذا البحث، تستطيع الحواسيب من الناحية النظرية التعامل مع أشد المسائل صعوبة في زمن معقول. وقد كتب عالم الحاسوب البارز سكوت آرونسون من جامعة أوستن في مدونته: "لا أستطيع أن أتذكر شخصاً واحداً كان يتوقع هذا الأمر". وإذا اجتاز هذا العمل اختبارات الخبراء المستقلين، فسوف يكون واحداً من أكبر المفاجآت في علم الحواسيب النظري لهذا القرن.

التاريخ الطويل لصفوف التعقيد

منذ السبعينيات، كان علماء الحواسيب يحاولون تقسيم صفوف التعقيد إلى أقسام أكثر دقة، ولهذا كانوا يعملون على تعريف مشاكل أكثر تعقيداً من NP، وكان تدقيق الحل يتيح مجالاً للمزيد من التعقيد. وفي بعض الحالات، لم يكن تزايد الزمن مع طول هذه المسألة من الشكل الحدودي، بل من الشكل الأسّي. أي أن الأمور تصبح أكثر تعقيداً من أحجية السودوكو التي يُقدم حلها إليك.

وحتى يتمكن علماء الحواسيب من تصنيف هذه المسائل أيضاً، قاموا بابتكار ما يسمى بأنظمة الإثبات التفاعلي في الثمانينيات؛ فقد تخيلوا حاسوباً جباراً يلعب دور "المُثبِت"، الذي يستطيع على الدوام تقديم حل لأية مهمة كانت، بغض النظر عن مدى تعقيدها. وبالتالي يستطيع أيضاً حساب المسائل التي تفوق أحاجي السودوكو في تعقيدها بكثير، وفي نفس الوقت يتمتع بقدرة تخزين لانهائية، ويستطيع إجراء عدد لانهائي من الحسابات من حيث المبدأ.

غير أن المُثبت ليس موثوقاً، ولهذا فنحن أيضاً في حاجة إلى "فاحِص" لإعادة حساب النتيجة؛ ففي السودوكو، يقوم هذا الجهاز بتأكيد صحة الحل. وخلافاً للمُثبت، فإن الفاحص عبارة عن حاسوب واقعي محدود الموارد، ما يعني أن زمن حساباته قد يعتمد على حجم المهمة بشكل حدودي.

قد يكون حل المثبت طويلاً ومعقداً للغاية، ولهذا فإن الفاحص يسأله عدة أسئلة محاولاً "إقناع نفسه" بصحة الحل. ويمكن أن نشبه الوضع بطاولة في غرفة مظلمة؛ حيث توجد عدة كتل خشبية متطابقة الشكل، ويُطلب تصنيفها حسب اللون. وبما أن المثبت يتمتع بقدرات خارقة، فلن يواجه أية صعوبة في هذه المهمة، وسيقوم بتوزيع الكتل على كومتين. الآن، يجب على الفاحص أن يتحقق من صحة الحل باختيار كتلتين من الكومتين يشكل عشوائي، والسؤال عما إذا كانتا فعلاً مختلفتين في اللون. وفي هذه الحالة، يمكن أن يقول المثبت إن إحداهما حمراء والأخرى زرقاء. ولكن هل هذا صحيح؟ أم أن المثبت يكذب؟ للتحقق من هذا، يقوم الفاحص بإخفاء الكتلتين الخشبيتين ومبادلتهما وسؤال المثبت عن الكتلة الحمراء. فإذا تم تكرار التجربة عدداً كافياً من المرات، فسيكون المثبت مخطئاً حوالي نصف عدد المرات إذا كان يكذب، أو على حق طوال الوقت إذا كان يقول الحقيقة.

استجواب لعدة مشبوهين

وجد علماء الحاسوب أنه لا يمكن التحقق من صحة حل بعض المهام إلا عن طريق إستراتيجية أسئلة مماثلة؛ فإذا أخذنا هذه المشاكل بعين الاعتبار، فإن تعقيد الصف NP يمتد إلى IP (interactive polynomial: صف المسائل القابلة للحل باستخدام نظام إثبات تفاعلي ويعادل الصف PSPACE، الذي يضم جميع مسائل القرار التي يمكن حلها بواسطة آلة تورنغ تستخدم كمية موارد حدودية). بل هناك حتى وسيلة للتعامل مع مسائل أكثر صعوبة، وذلك عن طريق استخدام عدة أنظمة فاحصة (MIP: multi-prover interactive proof)، بحيث يُسمح لها بتبادل الأفكار بين بعضها البعض أثناء العمل على مهمة ما، والفصل ما بينها بحيث تعمل بشكل مستقل أثناء تدقيق نتيجة ما. وبهذه الطريقة، يمكن أن يقوم الفاحص باستخدام إستراتيجية الأسئلة للتعامل مع مسائل أكثر صعوبة، وتدقيقها على الرغم من ذلك في زمن حدودي. ويصبح الأمر أسهل بالنسبة للفاحص إذا تمكن من توجيه الأسئلة عدة مرات، تماماً مثل ضابط الشرطة الذي يستطيع الحصول على المعلومات التي يريدها بعد عدة جلسات استجواب، وبهذا يمكن حل مسائل أكثر صعوبة بهذه الطريقة. ويتصف صف المسائل الموافق لهذه الحالة MIP بأنه أكثر تعقيداً من IP، كما اكتشف علماء الحاسوب في 1988.

بعد هذه النتيجة، وصل مجال أنظمة الإثبات التفاعلي إلى مرحلة من الاستقرار المؤقت. وعلى الأقل، إلى أن بدأ بعض الباحثين بالتساؤل عما سيحدث إذا كان المُثبت حاسوبين كموميين بدلاً من أن يكونا حاسوبين تقليديين متصلين فيما بينهما عن طريق الفيزياء الكمومية، وهو أمر ممكن بفضل ظاهرة التشابك الكمومي، التي كانت تثير قلق أينشتاين في ذلك الوقت. أطلق أينشتاين على هذه الظاهرة اسم "الفعل الشبحي عن بعد"؛ لأن قياس حالة أحد الجسمين المتشابكين يؤثر على حالة الجسم الآخر، بغض النظر عن المسافة الفاصلة بينهما. وفي البداية، سبَّب هذا للفيزيائيين بعضَ الارتباك والقلق، ولكننا نعلم الآن أنه لا يمكن نقل المعلومات بهذه الطريقة.

في البداية، لم يُلقِ الباحثون في مجال التعقيد بالاً إلى موضوع المُثبتات المتشابكة، بما أنهم كانوا يفترضون أن صف التعقيد الموافق لها هو MIP*، وهو أصغر من MIP وحتى من IP؛ حيث إن أفضلية MIP تكمن في توجيه الأسئلة إلى الحواسيب الخارقة بشكل منفصل، فإذا كانت الحواسيب المثبتة متشابكة، فإن الإجابة التي سيحصل عليها أحد هذه الحواسيب سيؤثر على حالة الآخر. ويستذكر عالم الحاسوب توماس فيديك من معهد كاليفورنيا للتكنولوجيا، والمؤلف المشارك في البحث المنشور في مجلة QUANTA MAGAZINE العام الماضي، قائلاً: "كانت ردة الفعل الطبيعية لدى الجميع، بما فيهم أنا شخصياً، هي زيادة استطاعة المُثبت". وأخيراً، يمكن للمثبتات استخدام التشابك لتنسيق استجاباتها عند التعرض للاستجواب من قبل الفاحص.

استخدام الحواسيب الكمومية المتشابكة كحل

ولكن، في 2012، ظهرت المفاجأة الكبرى الأولى، فقد أثبت فيديك وزميله تسيويوشي أيتو من جامعة واترلو أنه يمكن استخدام الحواسيب الكمومية المتشابكة للتحقق من جميع المسائل من الصف MIP في زمن حدودي، وبذلك يكون كلا صفي التعقيد على الأقل من نفس الحجم. أما المفاجأة الثانية فقد ظهرت في 2019؛ حيث اكتشف الفيزيائيان أناند ناتاراجان من معهد كاليفورنيا للتكنولوجيا وجون رايت من معهد ماساتشوستس للتكنولوجيا أن الحاسوب الكمومي من الصف MIP* أكبر حتى من الصف MIP. وبالتالي فإن التشابك ليس بالضرورة عائقاً، بل يمكن حتى للمُدقق استخدام هذه الميزة لصالحه، وتدقيق المسائل المعقدة بشكل أكثر من المتوقع.

تكمن الحيلة في استخدام التشابك لتحديد الأسئلة المناسبة، أي أن أجهزة المُثبت توجه الأسئلة إلى نفسها أولاً. قد يبدو هذا للوهلة الأولى مصدر تناقض، ولكن نظراً للتشابك بين المُثبتَين، فإنهما يستطيعان التعامل مع عدة أجوبة في نفس الوقت، وبالتالي التعامل مع المزيد من خطوات التدقيق، ويقومان بتقديم هذه الأسئلة إلى الفاحص.

خلال الاختبار الفعلي، يتعين على النظام ضمان أن الأسئلة تمثل المعنى المطلوب منها بشكل فعلي، وأن الأجوبة لا تؤدي إلى تناقضات. وبهذه الطريقة، يمكن إجراء الاختبار في زمن معقول، وهو زمن يتزايد حدودياً مع حجم المسألة.

إستراتيجية "الأسئلة المترابطة" هذه تعني أنه يمكن التحقق من الإثبات بسرعة أكبر، غير أن هذا يتطلب المزيد من الحرص على عدم تشابك الأجوبة التي تقدمها المثبتات، وإلا فسيتحول الوضع إلى ما يشبه تعاوناً مريباً بين مشتبهين اثنين أثناء الاستجواب. وقد حل ناتاراجان ورايت هذه المعضلة باستخدام مفهوم غريب آخر من عالم الميكانيك الكمومي، وهو الارتياب الكامن في العالم متناهي الصغر؛ حيث يستحيل تحديد خاصتين "متتامتين" لجسم ما، مثل الموضع وكمية الحركة، بشكل مقصود في نفس الوقت، فإذا قمت بقياس سرعة جسيم ومن ثم قمت بتحديد موضعه، ستجد عندها أنك لم تعد تعرف سرعته. ولهذا لا يُسمح للمثبتات إلا بإجراء قياسات متتامة، بحيث لا تؤثر على بعضها البعض. فإذا طلبت من الحاسوب الكمومي الأول قيمة حسابية، فسيؤدي هذا إلى إلغاء المعلومة الموافقة من الحاسوب الكمومي الآخر.

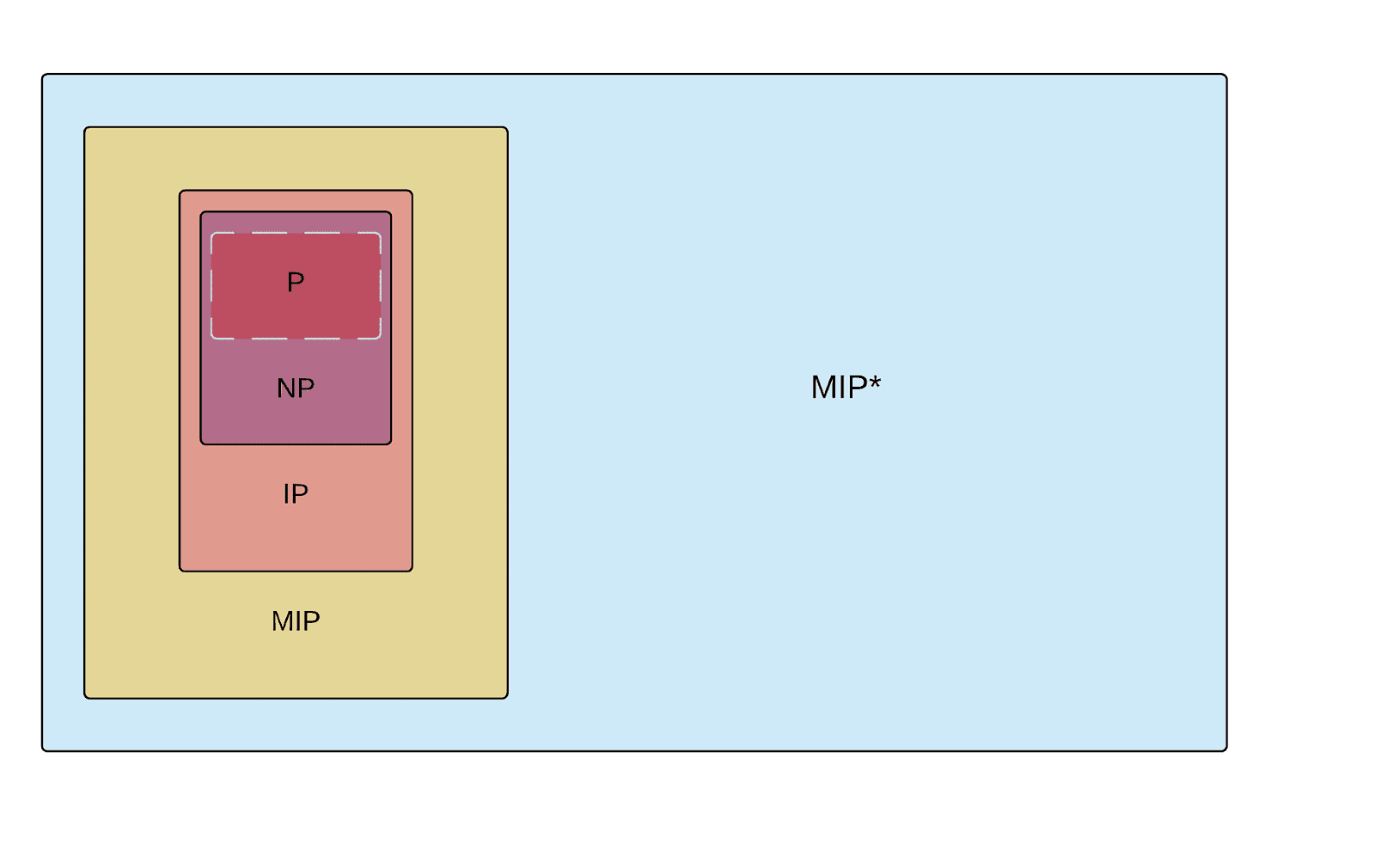
يدرك علماء الحواسيب الآن أن الصف MIP* يتخطى تعقيد MIP. ولكن مدى اتساع هذا الصف فعلياً لم يكن واضحاً في البداية؛ فإلى أي مدى سيصبح تدقيق الحلول أفضل إذا تم استجواب الحواسيب الكمومية المتشابكة؟ في الواقع، يبدو أن هذه الطريقة تؤدي إلى زيادة عدد المهام. وكما أثبت زينغفينج جي مع ناتاراجان وفيديك ورايت وهنري يوين من جامعة تورونتو في بحثهم المثير الذي نُشر مطلع هذا العام، فإن الصف MIP* يحتوي على جميع المسائل القابلة للحساب في علم الحاسوب.

وفقاً للإثبات، فإن MIP* مطابق لصف التعقيد الضخم RE (recursively enumerable: القابل للعد بشكل عَوديّ)، ويتضمن جميع مسائل القرار (التي تحتمل إجابتين فقط: نعم ولا) التي يستطيع الحاسوب (آلة تورنغ) الإجابة عنها في زمن منتهٍ. وهذا يتضمن مسألة التوقف الشهيرة، التي تهدف إلى تحديد ما إذا كان حاسوب ما سيتوقف أثناء حساب مهمة ما، أو سيستمر بإجراء الحسابات إلى الأبد.

أثبت عالم الحاسوب البريطاني ألان تورنغ عام 1936 أنه لا توجد خوارزمية تستطيع حساب مسألة التوقف بشكل عام؛ غير أن هذا لا يتناقض مع بحث جي وزملائه. يقول عمل جي وزملائه إن الفاحص التقليدي يمكن أن يتحقق خلال زمن حدودي من نتائج مُثبتَين خارقين كموميين متشابكين يقولان إن حاسوباً ما سيتوقف عن إجراء الحسابات في مهمة ما.

مفاجأة غير متوقعة بالنسبة للرياضيين

هذا أمر مذهل بحد ذاته، ولكن هذه النتائج التي توصل إليها علماء الحواسيب ستؤثر أيضاً على الرياضيات والفيزياء الكمومية. وكنتيجة لهذا، فقد تبين أن "مسألة الإدماج" -التي صاغها الفائز بجائزة فيلدز ألان كون في السبعينيات- خاطئة، وهو ما لم يتوقعه الكثير من العلماء. وبالتالي، فإن الكثير من الفرضيات الأخرى التي تعتمد عليها خاطئة أيضاً.

تتعامل مسألة الإدماج مع جبر المؤثِّرات (operator aljebra) –إضافة إلى أشياء أخرى- وهو الذي ينتمي إلى مجال في الرياضيات يسمى بتحليل التوابع، غير أنها تظهر في ميكانيك الكم أيضاً. وفي الواقع، توجد معلومة فيزيائية تكافئ مسألة كون، وهي أنه يمكن تقريب جميع الترابطات الممكنة في ميكانيك الكم إلى أية دقة مرغوبة باستخدام عدد محدود من الكيوبتات المتشابكة. وخلافاً لما توقعه معظم العلماء، فإن النتيجة التي توصل إليها علماء الحاسوب النظريون تبين أن هذا الادعاء خاطئ.

سيؤدي هذا إلى نتائج هامة في العديد من المواضيع، مثل الفرق ما بين الأنظمة المنتهية واللانهائية. وخلافاً لما يُفترض في أغلب الأحيان، لا يمكن تقريب نظام لانهائي على الدوام وفق دقة مختارة مسبقاً باستخدام نظام منتهٍ. وفي بحثهم هذا، قدم جي وزملاؤه مثالاً عن وضع يتضمن شخصين يلعبان لعبة، فإذا كانا متشابكين بشكل لانهائي، فإنهما سيفوزان باحتمال يساوي الواحد، أما إذا كان التشابك محدوداً، فإن احتمال الفوز يساوي النصف على الأكثر. وعلى عكس المتراجحات التي صاغها جون بيل في الستينيات، لا يمكن اختبار لعبة كهذه في المختبر؛ حيث لا يوجد إمكانية لتشابك لانهائي بين نظامين. ولكن هذا العمل يثبت أن نظرية التعقيد -وعلى عكس ما يزعم البعض- مجالٌ مستقل بحد ذاته، ولكنه يؤثر على مسائل أخرى، حتى لو كانت مجردة مثل الفيزياء الكمومية النظرية.